Schematic Diagrams, DC circuits

This is a source of emf (electromotive force), with a voltage of , measured in units of volts, V. The most common source you will see will be a battery.

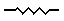This is a resistance, measured in units ohms ohms, . Most often it will be a resistor. However, wires connecting parts of a circuit are really not resistance-free. We can model this real-life case by putting a 'resistor' in the circuit which has the same resistance as the wires would have. Thus the wires can still be considered resistance-free since their resistance is represented by an additional resistor.

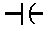This is a capacitor, with capacitance C measured in units of farads, F. The perfect capacitor will have no resistance (or inductance; see next), and we will assume that this symbol represents such an ideal capacitor. If a capacitor is not ideal, that is, it has some resistance (or inductance) associated with it, then we can model this by putting a 'resistor' (or inductor) in parallel with the capacitor. This resistor (or inductor) will have the same resistance (or inductance) as the non-ideal capacitor.

This is an inductor, with inductance L, measured in units of henrys, H. To model a non-ideal inductor in a circuit (an inductor with an associated resistance or capacitance) we can put a resistor in series or a capacitor in parallel with the inductor. Giving these the same values as the inductor will represent an imperfect inductor.

--------------------------------------------------------------

1. Ohm's Law deals with the relationship between voltage and current in an ideal conductor. This relationship states that:

The potential difference (voltage) across an ideal conductor is proportional to the current through it.

The constant of proportionality is called the "resistance", R.

Ohm's Law is given by:

V = I R

where V is the potential difference between two points which include a resistance R. I is the current flowing through the resistance. For biological work, it is often preferable to use the conductance, g = 1/R; In this form Ohm's Law is:

I = g V

2. Material that obeys Ohm's Law is called "ohmic" or "linear" because the potential difference across it varies linearly with the current.

3. Ohm's Law can be used to solve simple circuits. A complete circuit is one which is a closed loop. It contains at least one source of voltage (thus providing an increase of potential energy), and at least one potential drop i.e., a place where potential energy decreases. The sum of the voltages around a complete circuit is zero.

4. An increase of potential energy in a circuit causes a charge to move from a lower to a higher potential (ie. voltage). Note the difference between potential energy and potential.

Because of the electrostatic force, which tries to move a positive charge from a higher to a lower potential, there must be another 'force' to move charge from a lower potential to a higher inside the battery. This so-called force is called the electromotive force, or emf. The SI unit for the emf is a volt (and thus this is not really a force, despite its name). We will use a script E, the symbol , to represent the emf.

A decrease of potential energy can occur by various means. For example, heat lost in a circuit due to some electrical resistance could be one source of energy drop.

Because energy is conserved, the potential difference across an emf must be equal to the potential difference across the rest of the circuit. That is, Ohm's Law will be satisfied:

= I R

5. Here is a nice simulated experiment on Ohm's Law for you to test your understanding of this concept. Use the "back" button to return to this place.

Source : http://www.physics.uoguelph.ca/tutorials/ohm/